关键词 激活 GaAs光电阴极 双偶极子模型 光谱响应
毕业论文设计说明书外文摘要
Title Optimization of Cs-O activation process of GaAs photocathodes
Abstract
Based on learning the GaAs surface model, using information measurement and control system, this paper performed two groups of experiments about optimization of Cs-O activation process of GaAs photocathodes .The first groups of experiments were compared three different activation methods and the activation process, spectral response and stability difference. We found that the photocathode activated in Cs source continuous and O source discontinuous has higher sensitivity, better stability, and stronger longwave response. The second group of experiments is based on Cs source continuous and O source discontinuous activation, comparing the different Cs/O ratio activation process, spectral response and stability differences of influence. We found that Only the appropriate Cs/O ratio can make the activation curve with good symmetry, alternate time short, photocurrent increased a lot. Possible mechanism was tentatively discussed with a double dipole model. And we found that a slight excess of Cs improves performance of the photocathode. We suggest that careful control of Cs quantity plays a key role in GaAs photocathode activation.
Keywords Activation GaAs photocathode Double dipole model Spectral response
目 次
1 绪论1
1.1 GaAs光电阴极概况1
1.2 GaAs光电阴极表面模型4
1.3 本论文的研究意义与主要工作6
2 负电子亲和势光电阴极制备和评估系统7
2.1 超高真空激活系统7
2.2 多信息量在线监控系统的组成9
2.3 激活软件介绍11
3 不同激活方式对GaAs光电阴极的影响研究13
3.1 不同激活方法介绍13
3.2 实验准备14
3.3 实验结果14
3.4 分析与讨论18
4 铯氧比对GaAs光电阴极激活过程的影响研究20
4.1 实验准备20
4.3 实验结果21
4.4 分析与讨论24
5 结论26
致谢27
参考文献28
1 绪论
1.1 GaAs光电阴极概况
1.1.1 GaAs光电阴极的原理与发现
外光电效应,也称光电发射,光线照射在金属表面会使其发射出电子的物理效应[1],如图1.1所示。光电效应发生的条件是入射光的频率超过金属的极限频率,光子能量减去功函数所剩下的能量将会称为发射电子的动能,方程为Ek = hν-Φ[1]。
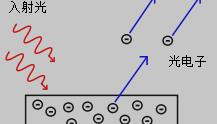
图 1.1 光电效应示意图
爱因斯坦对此现象进行过多次实验,他发现,材料内部的电子吸收了入射光的能量,有足够大的能量克服材料表面的势垒而逸出,这是光能转化为电能的一种形式,也是非常重要的电子发射形式[2]。我们把能发生此类效应的材料称为光电阴极,为了寻找合适的光电阴极,近代许多科研工作者努力研究开发最合适的材料。在二十世纪五十年代左右,研究者们发明了这几种光电阴极[3]:银-氧-铯光电阴极(Ag-O-Cs,S-1,1930),铯-锑-钾光电阴极(Cs3Sb,S-11,1936),铋-银-氧-铯光电阴极(Bi-Ag-O-Cs,S-10,1938),钠-钾-锑光电阴极(Na2KSb,1955),钠-钾-锑-铯光电阴极(Na2KSb[Cs],S-20,1955)和钾-铯-锑光电阴极(K2CsSb,1963)。
下一篇:粉粒体填充床流动过程实验研究